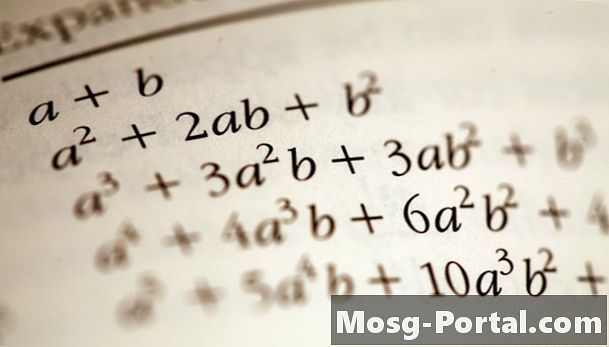
Tartalom
- TL; DR (túl hosszú; nem olvastam)
- A binomiális kocka kiszámítása
- Mi a helyzet a kivonással?
- Vigyázz a kockák összegére és különbségére
Az Algebra tele van olyan ismétlődő mintákkal, amelyeket minden alkalommal számtani módszerrel dolgozhatott ki. De mivel ezek a minták annyira általánosak, általában egyfajta képletet alkalmaznak a számítások megkönnyítésére. A binomiális kocka kiváló példa: Ha minden alkalommal ki kellett dolgoznia, sok időt töltsön ceruzával és papírral fárasztva. De ha már ismeri a kockának a megoldására szolgáló képletet (és néhány hasznos trükköt annak emlékezetéhez), a válasz megtalálása olyan egyszerű, mint a megfelelő kifejezések beillesztése a megfelelő változó nyílásokba.
TL; DR (túl hosszú; nem olvastam)
A binomiális kocka képlete (egy + b):
(egy + b)3 = egy3 + 3_a_2b + 3_ab_2 + b3
A binomiális kocka kiszámítása
Nem kell pánikba esnie, ha olyan problémát látsz (a + b)3 veled szemben. Miután lebontotta az ismerős alkotóelemeire, úgy tűnik, hogy jobban ismeri a matematikai problémákat, amelyeket korábban tettél.
Ebben az esetben segít megjegyezni ezt
(a + b)3
ugyanaz mint
(a + b) (a + b) (a + b), amelynek sokkal ismeretlenebbnek kell kinéznie.
Ahelyett, hogy minden alkalommal kidolgozta volna a matematikát, használhatja egy olyan képlet "parancsikonját", amely a választ kapja. Itt egy képi képlet képlete:
(a + b)3 = a3 + 3a2b + 3ab2 + b3
A képlet használatához azonosítsa, mely számok (vagy változók) foglalják el az egyenlet bal oldalán az "a" és "b" réseket, majd cseréljék ki ugyanazokat a számokat (vagy változókat) az "a" és "b" résekre a képlet jobb oldalán.
1. példa: megfejt (x + 5)3
Amint látod, x az "a" helyet foglalja el a képlet bal oldalán, és az 5 a "b" helyet foglalja el. Behelyettesítve x és 5. ábra a képlet jobb oldalán adja meg:
x3 + 3x25 + 3x52 + 53
Egy kissé egyszerűsítve közelebb kerül a válaszhoz:
x3 + 3 (5) x2 + 3 (25) x + 125
És végül, miután egyszerűen egyszerűsítette a lehetőségeket:
x3 + 15x2 + 75x + 125
Mi a helyzet a kivonással?
Nem kell másképlet egy olyan probléma megoldásához, mint például (y - 3)3. Ha emlékszel erre y - 3 ugyanaz mint y + (-3), egyszerűen átírhatja a problémát 3 és oldja meg az ismerős képlettel.
2. példa: megfejt (y - 3)3
Mint már említettük, az első lépés a probléma átírása 3.
Ezután emlékezzen meg a kétszeri binomiális képletére:
(a + b)3 = a3 + 3a2b + 3ab2 + b3
A problémádban, y az "a" rést az egyenlet bal oldalán, és -3 az "b" rést foglalja el. Helyezze ezeket a megfelelő résekbe az egyenlet jobb oldalán, különös figyelmet fordítva a zárójelre, hogy megőrizze a negatív jelet a -3 előtt. Ez megadja neked:
y3 + 3y2(-3) + 3y (-3)2 + (-3)3
Most itt az ideje az egyszerűsítéshez. Ismét figyeljen arra a negatív jelre, amikor exponenteket alkalmaz:
y3 + 3 (-3) y2 + 3 (9) y + (-27)
Még egy egyszerűsítési kör adja meg a választ:
y3 - 9y2 + 27y - 27
Vigyázz a kockák összegére és különbségére
Mindig ügyeljen arra, hogy hol vannak a problémák. Ha problémát lát az űrlapon (a + b)3vagy 3, akkor az itt tárgyalt képlet megfelelő. De ha a problémád néz ki (a3 + b3) vagy (a3 - b3), nem a binomiális kocka. Ez a kockák összege (az első esetben) vagy a kockák különbsége (a második esetben), amely esetben a következő képletek egyikét alkalmazza:
(a3 + b3) = (a + b) (a2 - ab + b2)
(a3 - b3) = (a - b) (a2 + ab + b2)