Az ellipszist a sík geometriájában úgy definiálhatjuk, mint a pontok halmaza, hogy a két ponttal (fókuszokkal) mért távolságok összege állandó legyen. A kapott ábra nem matematikailag is leírható ovális vagy "ellapított kör" alakban. Az ellipszisek számos alkalmazásban vannak a fizikában, és különösen hasznosak a bolygó körüli pályák leírására. Az excentrikusság az ellipszis egyik jellemzője és azt jelzi, hogy az ellipszis milyen kör alakú.
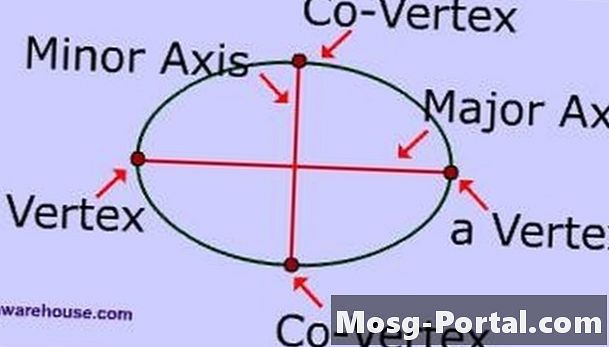
Vizsgálja meg az ellipszis részeit. A főtengely a leghosszabb vonalszakasz, amely keresztezi az ellipszis középpontját, és végpontjai az ellipszisön vannak. A melléktengely a legrövidebb vonalszakasz, amely keresztezi az ellipszis középpontját, és amelynek végpontjai vannak az ellipszisnél. A fő féltengely a főtengely felének, a másodlagos féltengely pedig a melléktengely felének.
Vizsgálja meg az ellipszis képletét. Az ellipszis matematikai leírására számos különféle módszer létezik, de az excentricitás kiszámításához az ellipszis számára a leghasznosabb: x ^ 2 / a ^ 2 + y ^ 2 / b ^ 2 = 1. Az a és az állandók b értékei egy adott ellipszisre vonatkoznak, és a változók az ellipszisön fekvő pontok x és y koordinátái. Ez az egyenlet egy ellipszist ír le, amelynek középpontja az eredeti és a fő- és melléktengely, amely az x és y origón fekszik.
Azonosítsa a féltengelyek hosszát. Az x ^ 2 / a ^ 2 + y ^ 2 / b ^ 2 = 1 egyenletben a féltengelyek hosszát a és b adja meg. A nagyobb érték a fő féltengelyt, a kisebb pedig a kisebb féltengelyt képviseli.
Számítsa ki a fókusz helyzetét. A fókuszok a főtengelyen vannak, a központ mindkét oldalán. Mivel az ellipszis tengelye a kiindulási vonalakon fekszik, az egyik koordinátája mindkét fókuszra 0 lesz. A másik koordináta a (a ^ 2 - b ^ 2) ^ (1/2) lesz az egyik fókusz esetében és - (a ^ 2 - b ^ 2) ^ (1/2) a többi fókuszhoz, ahol a> b.
Számítsa ki az ellipszis excentricitását a fókusz távolsága és a középpont távolsága arányában a félig nagyobb tengely hosszával. Az e excentricitás tehát (a ^ 2 - b ^ 2) ^ (1/2) / a. Vegye figyelembe, hogy 0 <= e <1 minden ellipszisnél. A 0 excentritása azt jelenti, hogy az ellipszis egy kör, egy hosszú, vékony ellipszis excentritása megközelíti az 1-t.