Tartalom
- Mechanikai előny
- Az energiamegőrzési törvény
- Differenciálmű csiga
- Newtoni második törvény
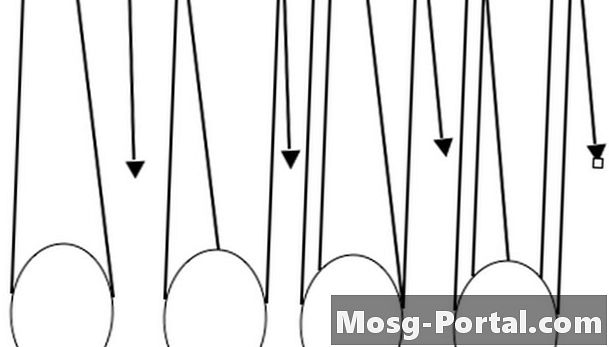
- Több függő blokk
Számos érdekes helyzetet állíthatunk fel a szíjtárcsákkal annak ellenőrzésére, hogy a hallgatók megértsék-e a Newton második mozgási törvényét, az energiamegtakarítás törvényét és a fizikai munka meghatározását. Az egyik különösen oktató helyzet megtalálható az úgynevezett differenciálmű tárcsán, amely a szerszámok, amelyeket a mechanikus üzletekben nehéz emelőkben használnak.
Mechanikai előny
Mint egy kar esetében, az erő kifejtett távolságának növelése a teher felemelésének távolságához képest növeli a mechanikai előnyt vagy a tőkeáttételt. Tegyük fel, hogy két tárcsablokk van használatban. Az egyik rakományhoz kapcsolódik; az egyik a fenti tartóhoz kapcsolódik. Ha a rakományt X egységekkel kell megemelni, akkor az alsó tárcsablokknak az X egységeket is fel kell emelnie. A fenti szíjtárcsa nem mozog fel vagy le. Ezért a két szíjtárcsa közötti távolságnak le kell rövidítenie az X egységeket. A két szíjtárcsa között hurkolt vonal hossza mindegyikének le kell rövidítenie az X egységeket. Ha vannak Y ilyen vonalak, akkor a lehúzónak X --- Y egységeket kell húznia az X rakományegységek felemeléséhez. Tehát a szükséges erő a terhelés súlyának 1 / Y-szerese. A mechanikai előnye Y: 1.
Az energiamegőrzési törvény
Ez a tőkeáttétel az energiamegtakarítás törvényének eredménye. Emlékezzünk arra, hogy a munka egyfajta energia. Munkánk alatt a fizikai meghatározást értjük: az erő, amelyet egy terhelés és a távolság közötti távolságra gyakorolunk, amelyen a terhet az erő mozgatja. Tehát, ha a rakomány Z Newton, az X egységek felemeléséhez szükséges energiának meg kell egyeznie a húzó által végzett munkával. Más szavakkal, Z --- X-nek egyenlőnek kell lennie (a húzó által kifejtett erő) --- XY. Ezért a lehúzó által kifejtett erő Z / Y.
Differenciálmű csiga
Érdekes egyenlet akkor merül fel, ha a vonalat folytonos hurokká tesszük, és a tartóból lógó blokknak két szíjtárcsa van, az egyik kissé kisebb, mint a másik. Tegyük fel azt is, hogy a blokkban lévő két görgő úgy van rögzítve, hogy együtt forogjanak. Hívja az "R" és "r" szíjtárcsa sugarait, ahol R> r.
Ha a lehúzó elegendő vonalt húz ki ahhoz, hogy egy rögzített forgáson keresztül forgassa a rögzített tárcsákat, akkor kihúzta a 2πR vonalot. A nagyobb szíjtárcsa ezután 2πR vonalon vett el a teher támogatását. A kisebb szíjtárcsa ugyanabba az irányba forog, és 2πr vonalot enged ki a rakományhoz. Tehát a terhelés 2πR-2πr-rel megemelkedik. A mechanikai előny a meghúzott távolság elosztása a megtett távolsággal, vagy 2πR / (2πR-2πr) = R / (R-r). Vegye figyelembe, hogy ha a sugarak csak 2% -kal különböznek, akkor a mechanikai előny egy óriási 50: 1.
Egy ilyen szíjtárcsát differenciális szíjtárcsának hívnak. Ez egy gyakori szerelvény az autójavító műhelyekben. Érdekes tulajdonsága, hogy a vonó, amelyet húz, húzódhat, amikor a teher alul van tartva, mert mindig van elég súrlódás, hogy a két tárcsa ellentétes erői megakadályozzák annak elfordulását.
Newtoni második törvény


Tegyük fel, hogy két blokk van csatlakoztatva, és egy, M1-nek hívódik, egy szíjtárcsa lóg le. Mennyire gyorsulnak fel? Newtoni második törvény az erőre és a gyorsulásra vonatkozik: F = ma. A két blokk tömege ismert (M1 + M2). A gyorsulás ismeretlen. Az erő az M1 gravitációs vonzása alapján ismert: F = ma = M1 --- g, ahol g a gravitációs gyorsulás a Föld felszínén.
Ne feledje, hogy az M1 és az M2 együtt gyorsul. Az a) gyorsulás megtalálása csak az F = ma képlet helyettesítésének kérdése: M1 --- g = (M1 + M2) a. Természetesen, ha az M2 és az asztal közötti súrlódás az egyik olyan erő, amelynek F = M1 --- g-nek ellen kell állnia, akkor ezt az erőt könnyen hozzá kell adni az egyenlet jobb oldalához is, az a) gyorsulás előtt megoldva.
Több függő blokk

Mi van, ha mindkét blokk lóg? Akkor az egyenlet bal oldalán két kiegészítés van, nem csupán egy. A könnyebb a keletkező erő ellenkező irányába halad, mivel a nagyobb tömeg határozza meg a két tömegű rendszer irányát; ezért a kisebb tömegre eső gravitációs erőt le kell vonni. Tegyük fel, hogy M2> M1. Ezután a fenti bal oldali oldal M1 --- g értékről M2 --- g-M1 --- g értékre változik. A jobb oldali változatlan marad: (M1 + M2) a. Az a) gyorsulást ezután számtanilag triviálisan oldják meg.