Tartalom
- Párhuzamos áramkör diagram
- tippek
- Párhuzamos áramköri példák
- Párhuzamos és soros áramkör
- Soros-párhuzamos áramkör
Az elektromos áramkörök áramköri elemeit sorba vagy párhuzamosan lehet elrendezve. Soros áramkörökben az elemeket ugyanazzal az ággal kapcsolják össze, amely egyenként egyenként továbbítja az elektromos áramot. Párhuzamos áramkörökben az elemeknek külön elágazásuk van. Ezekben az áramkörökben az áram egész útvonalon eltérő lehet.
Mivel az áram különböző útvonalakat vehet fel egy párhuzamos áramkörben, az áram nem állandó az egész párhuzamos áramkörben. Ehelyett az egymással párhuzamosan összekapcsolt ágak esetében az egyes ágok feszültség- vagy potenciálcsökkenése állandó. Ennek oka az, hogy az áram eloszlik az egyes ágak között olyan mennyiségben, amely fordítottan arányos az egyes ágak ellenállásával. Ennek következtében az áram van a legnagyobb, ahol az ellenállás a legkisebb, és fordítva.
Ezek a tulajdonságok lehetővé teszik, hogy a párhuzamos áramkörök lehetővé tegyék a töltés áramlását két vagy több útvonalon, ezáltal a háztartásokban és az elektromos készülékekben egy stabil és hatékony áramellátási rendszeren keresztül szabványos jelölt. Ez lehetővé teszi az áram áramlását az áramkör más részein, ha egy rész megsérül vagy megszakad, és egyenlően képesek elosztani az energiát a különböző épületek között. Ezeket a jellemzőket diagrammal és egy párhuzamos áramkör példájával lehet bebizonyítani.
Párhuzamos áramkör diagram
tippek
Párhuzamos áramköri példák
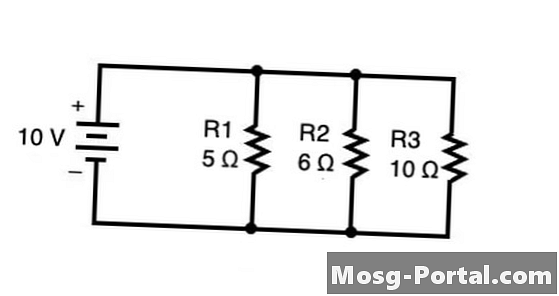
Az egymással párhuzamosan elrendezett ellenállások teljes ellenállásának meghatározásához használja a képletet 1 / Rteljes = 1 / R1 + 1 / R2 + 1 / R3 + ... + 1 / Rn amelyben az ellenállások ellenállását az egyenlet jobb oldalán összegzik. A fenti diagramban a teljes ellenállás ohmban (Ω) a következőképpen számítható ki:
Ne feledje, hogy az egyenlet mindkét oldalát csak "átfordíthatja" a 3. lépésről a 4. lépésre, ha az egyenlet mindkét oldalán csak egy kifejezés van (ebben az esetben 1 / Rteljes balra és 14/30 Ω jobbra).
Az ellenállás kiszámítása után az áramerősség és a feszültség az Ohms törvény alkalmazásával kiszámítható V = I / R amiben V voltban mért feszültség, én az áram amprában mért, és R az ellenállás ohmban. Párhuzamos áramkörökben az egyes útvonalakon áthaladó áramok összege a forrásból származó teljes áram. Az áramkör minden ellenállásánál az áram kiszámítható az ellenállás feszültség és szorzó szorzata szorzatával. A feszültség állandó marad az áramkör egészében, tehát a feszültség az akkumulátor vagy a feszültségforrás feszültsége.
Párhuzamos és soros áramkör
••• Syed Hussain AtherSoros áramkörökben az áram az egész állandó, a feszültségcsökkenések az egyes ellenállások ellenállásától függenek, és a teljes ellenállás az egyes ellenállások összege. Párhuzamos áramkörökben a feszültség az egész állandó, az áram az egyes ellenállásoktól függ, és a teljes ellenállás inverzje az egyes ellenállások inverzének összege.
A kondenzátorok és induktorok felhasználhatók a töltés soros és párhuzamos áramkörökben történő időbeli változtatására. Egy soros áramkörben az összes kapacitancia az áramkör (a változó által megadott) C), a kondenzátor azon képessége, hogy tárolja a töltést az idő múlásával, az egyes kapacitások inverzióinak fordított összege, és teljes induktivitás (én), az induktorok azon képessége, hogy idővel feltöltődjenek, az egyes induktorok összege. Ezzel szemben egy párhuzamos áramkörben a teljes kapacitás az egyes kondenzátorok összege, és a teljes induktivitás inverze az egyes induktivitások inverzióinak összege.
A soros és a párhuzamos áramköröknek is eltérő funkciója van. Egy soros áramkörben, ha az egyik alkatrész megszakad, az áram szokásosan nem áramlik át az áramkörön. Párhuzamos áramkörben az egyes ágnyílások csak az ebben az ágban levő áramot állítják le. A többi ág továbbra is működni fog, mert az áram több útvonalat vehet át az áramkörön.
Soros-párhuzamos áramkör

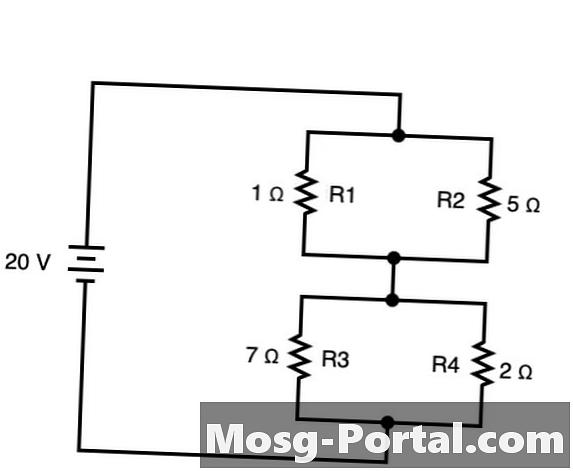
Azok az áramkörök, amelyeknek mindkét elágazó eleme van, és amelyek szintén össze vannak kötve úgy, hogy az áram egy irányban áramlik ezen ágak között mindkét sorozat és párhuzamos. Ezekben az esetekben mind sorozatból, mind párhuzamosan alkalmazhat szabályokat az áramkör számára. A fenti példában R1 és R2 párhuzamosan vannak egymással, hogy kialakuljanak R5, és így vannak R3 és R4 alkotnak R6. Ezeket párhuzamosan a következőképpen lehet összegezni:
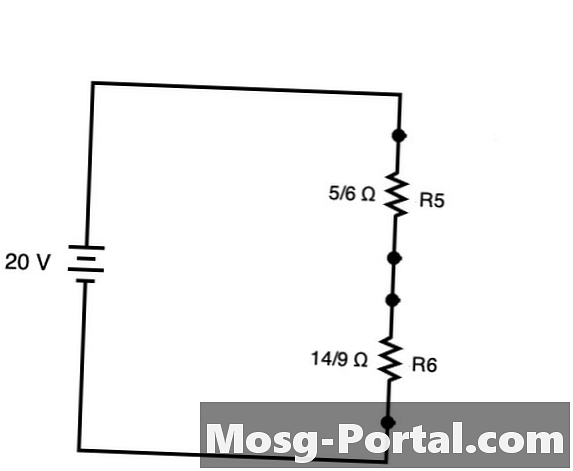
Az áramkört egyszerűsíteni lehet a fentiekben bemutatott áramkör létrehozásával R5 és R6. Ez a két ellenállás egyszerűen hozzáadható, mintha az áramkör soros lenne.
Rteljes = 5/6 Ω + 14/9 Ω = 45/54 Ω + 84/54 Ω = 129/54 Ω = 43/18 Ω vagy körülbelül 2,38 Ω
20-val V feszültségként az Ohms törvény azt diktálja, hogy a teljes áram megegyezik V / Rvagy 20 V / (43/18 Ω) = 360/43 A vagy kb 8,37 A. Ezzel az összárammal az Ohms törvény segítségével meghatározhatja az feszültségcsökkenést mind az R5, mind az R6 között.V = I / R) is.
Ért,-ra,-re, mert, mivelhogy R5, V5 = 360/43 A x 5/6 Ω = 1800/258 V vagy kb 6,98 V.
Ért,-ra,-re, mert, mivelhogy R6, V6 = 360/43 A x 14/9 Ω = 1680/129 V vagy kb 13.02 V.
Végül ezek a feszültségek csökkennek R5 és R6 osztható vissza az eredeti párhuzamos áramkörökbe az áramáram kiszámításához R1 és R2 ért,-ra,-re, mert, mivelhogy R5 és R2 és R3 ért,-ra,-re, mert, mivelhogy R6 az Ohms törvény alkalmazásával.
I1 = (1800/258 V) / 1 Ω = 1800/258 A vagy 6.98 A._
I2 = (1800/258 V) / 5 Ω = 1500/43 A vagy 34.88 A.
I3 = (680/129 V) / 7 = 4760/129 A vagy kb 36,90 A.
I3 = (680/129 V) / 2 Ω = 1360/129 A vagy kb 10,54 A.