Az érintő egyike a három alapvető trigonometrikus függvénynek, a másik kettő szinusz és koszinus. Ezek a funkciók nélkülözhetetlenek a háromszögek tanulmányozásához, és a háromszög szögeit az oldalukhoz viszonyítják. Az érintő legegyszerűbb meghatározása a derékszögű háromszög oldalarányát használja, és a modern módszerek ezt a funkciót egy végtelen sorozat összegének fejezik ki. Az érintõk közvetlenül kiszámíthatók, ha a jobboldali háromszög oldalainak hossza ismert és más trigonometrikus függvényekbõl levezethetõ.
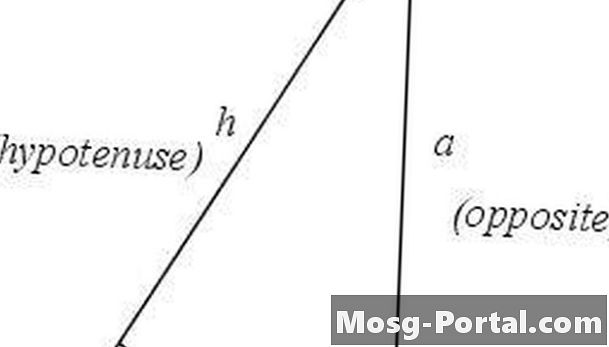
Azonosítsa és címkézze meg a derékszögű háromszög részeit. A derékszög a C csúcson helyezkedik el, és az ezzel szemben lévő oldal a h hipotenusz lesz. A θ szög az A csúcson, a fennmaradó csúcs pedig B. A angle szög melletti oldal b oldalú és opposite ellentétes oldal a az a oldal lesz. A háromszög két oldalát, amelyek nem a hipotenuszok, a háromszög lábainak nevezzük.
Határozza meg az érintőt. A szög érintőjét úgy határozzuk meg, hogy a szöget ellentétes oldal hosszának a szöget szomszédos oldal hosszához viszonyított aránya legyen. Az 1. lépésben leírt háromszög esetén tan θ = a / b.
Határozzuk meg az egyszerű derékszögű háromszög érintőjét. Például egy egyenlő szélességű háromszög lába egyenlő, tehát a / b = tan θ = 1. A szögek szintén egyenlők, tehát θ = 45 fok. Ezért barnul 45 fok = 1.
Mutassa be a tangenst a többi trigonometrikus függvénytől. Mivel a szinusz θ = a / h és a koszinusz θ = b / h, akkor a szinusz θ / koszinusz θ = (a / h) / (b / h) = a / b = tan θ. Ezért a tan θ = szinusz θ / koszinusz θ.
Számítsa ki az esetleges szög érintőjét és a kívánt pontosságot:
sin x = x - x ^ 3/3! + x ^ 5/5! - x ^ 7/7! + ... koszinusz x = 1 - x ^ 2/2! + x ^ 4/4! - x ^ 6/6! + ... Tehát tan x = (x - x ^ 3/3! + X ^ 5/5! - x ^ 7/7! + ...) / (1 - x ^ 2/2! + X ^ 4 / 4! - x ^ 6/6! + ...)