Az elektromos töltés kiszámítása

Tartalom

• Elektromos töltésképlet
• Elektromos töltés és gravitáció: hasonlóságok
• Az elektromos töltés megőrzése
• A töltött elektronok száma
• Az áramkörökben az elektromos töltés kiszámítása
• Elektromos mező képlet
• Az univerzum nettó töltése
• Az elektromos fluxus kiszámítása töltéssel
• Töltés és statikus áram
• Elektromos vezetők
• Gausss törvény más helyzetekben

Legyen szó statikus elektromosságról, amelyet egy szőrös kabát bocsát ki, vagy a televíziókat tápláló elektromos áramról, megismerheti az elektromos töltést a mögöttes fizika megértésével. A töltés kiszámításának módszerei maga a villamos energia jellegétől függenek, mint például annak elvei, hogy a töltés hogyan osztja el magát tárgyakon keresztül. Ezek az alapelvek ugyanazok, függetlenül attól, hogy hol vagy az univerzumban, és az elektromos töltés maga a tudomány alapvető tulajdonsága.

Elektromos töltésképlet

A számításnak sokféle módja van elektromos töltés különféle hátrányokhoz a fizikában és az elektrotechnikában.

Coulombs törvény általában az elektromos töltést hordozó részecskékből származó erő kiszámításához használják, és ez az egyik leggyakoribb elektromos töltési egyenlet. Az elektronok egyedi töltései -1602 × 10^-19 coulombs (C) és protonok ugyanolyan mennyiségű, de pozitív irányban, 1,602 × 10 ⁻¹⁹ C. Két díjért q₁ és q₂ _az távolság elválasztása _r, kiszámolhatja az elektromos erőt F_E a Coulombs törvény alapján generált:

F_E = frac {kq_1q_2} {r ^ 2}

amiben k egy állandó k = 9.0 × 10 ⁹ nm² / C². A fizikusok és a mérnökök néha használják a változót e egy elektron töltésére utalni.

Vegye figyelembe, hogy az ellenkező jelek (plusz és mínusz) töltése esetén az erő negatív, ezért vonzó a két töltés között. Ugyanazon jel két töltése esetén (plusz és plusz vagy mínusz és mínusz) az erő visszatükröződik. Minél nagyobb a töltés, annál erősebb a vonzó vagy visszataszító erő közöttük.

Elektromos töltés és gravitáció: hasonlóságok

A coulombs-i törvény a gravitációs erő tekintetében feltűnő hasonlóságot mutat a Newton-i jogszabályokkal F_{G ​} = G m₁m₂ / r² a gravitációs erő számára F_G, tömegek m₁és m₂és gravitációs állandó G = 6.674 × 10 ⁻¹¹ m³/ kg s². Mindketten különböző erőket mérnek, nagyobb tömeggel vagy töltéssel változnak, és függnek a két tárgy közötti sugáriránytól a második erőig. A hasonlóságok ellenére fontos megjegyezni, hogy a gravitációs erők mindig vonzóak, míg az elektromos erők vonzóak vagy visszatükrözőek lehetnek.

Azt is meg kell jegyeznie, hogy az elektromos erő általában sokkal erősebb, mint a gravitáció, a törvények állandóinak exponenciális ereje közötti különbségek alapján. A két törvény közötti hasonlóságok jobban megmutatják a szimmetriát és a mintákat az univerzum általános törvényei között.

Az elektromos töltés megőrzése

Ha egy rendszer izolált marad (azaz anélkül, hogy bármi mással érintkezne rajta kívül), akkor megtakarítja a töltést. A díj megőrzése azt jelenti, hogy az elektromos töltés teljes mennyisége (pozitív töltés mínusz negatív töltés) változatlan marad a rendszernél. A töltés megőrzése révén a fizikusok és a mérnökök kiszámíthatják, mennyi töltés mozog a rendszerek és a környezetük között.

Ez az elv lehetővé teszi a tudósoknak és a mérnököknek, hogy Faraday ketreceket hozzanak létre, amelyek fémes pajzsokkal vagy bevonattal vannak ellátva, hogy megakadályozzák a töltés kiszabadulását. A Faraday-ketrecek vagy a Faraday-pajzsok olyan elektromos mezőket használnak, amelyek hajlamosak az anyagon belüli töltések megoszlására, hogy kiküszöböljék a mező hatását, és megakadályozzák a töltések károsodását vagy belépését. Ezeket az orvosi berendezésekben, például a mágneses rezonancia képalkotó gépekben használják az adatok torzulásának megakadályozására, valamint a veszélyes környezetben dolgozó villanyszerelők és vonalvezetők védőberendezéseiben.

Kiszámolhatja a térfogat nettó töltési áramlását úgy, hogy kiszámítja a bevitt töltés teljes összegét, és kivonja a teljes távozó töltési mennyiséget. A töltést hordozó elektronokon és protonokon keresztül töltött részecskék hozhatók létre vagy pusztulhatnak el, hogy kiegyenlítsék magukat a töltés megőrzése mellett.

A töltött elektronok száma

Tudva, hogy egy elektron töltése -1,602 × 10 ⁻¹⁹ C, −8 × 10 töltés ⁻¹⁸ A C 50 elektronból állna. Ezt úgy találhatja meg, hogy elosztja az elektromos töltés mennyiségét az egyetlen elektron töltésének nagyságával.

Az áramkörökben az elektromos töltés kiszámítása

Ha tudod a elektromos áram, az elektromos töltés áramlása egy tárgyon, egy áramkörön áthaladás és az áram alkalmazásának időtartama, az elektromos töltés kiszámítható az áram egyenlete alapján Q = Azt amiben Q a coulombs-ban mért teljes töltés, én áram van erősítőben, és t az az idő, amikor az áramot másodpercben alkalmazzák. Használhatja az Ohms törvényt (V = IR) az áram kiszámításához a feszültségből és az ellenállásból.

Egy 3 V feszültségű és 5 resistance ellenállású áramkörnél, amelyet 10 másodpercig alkalmaznak, a megfelelő áram az eredmény én = V / R = 3 V / 5 Ω = 0,6 A, és a teljes töltés lenne Q = It = 0,6 A × 10 s = 6 C.

Ha ismeri a lehetséges különbséget (V) egy áramkörben alkalmazott feszültségben és a munka (W) annak alkalmazási ideje alatt készített džaulokban, a töltés coulombs-ban, Q = W / V.

Elektromos mező képlet

••• Syed Hussain Ather

Elektromos mező, az egy töltésenkénti elektromos erő sugárirányban kifelé terjed a pozitív töltésektől a negatív töltések felé, és ezekkel kiszámítható E = F_E / q, amiben F_E az elektromos erő és q az a töltés, amely az elektromos mezőt hozza létre. Tekintettel arra, hogy az alapvető mező és az erő hogyan számolódik az elektromosság és a mágnesesség szempontjából, az elektromos töltés az anyag tulajdonságaként határozható meg, amely a részecskének erőt okoz egy elektromos mező jelenlétében.

Még ha az objektum nettó vagy teljes töltése is nulla, az elektromos mezők lehetővé teszik a töltések eloszlását az objektumokon belüli különféle módon. Ha vannak benne díjeloszlások, amelyek nem nulla nettó töltést eredményeznek, akkor ezek az objektumok polarizált, és az a töltés, amelyet ezek a polarizációk okoznak, nevezik kötött díjak.

Az univerzum nettó töltése

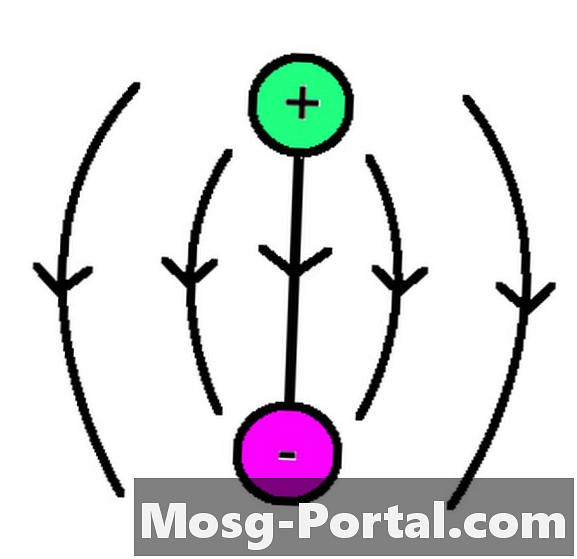
Bár a tudósok nem mindenki egyetértenek abban, hogy mi az univerzum teljes töltése, oktatott kitalálásokat készítettek és különféle módszerekkel tesztelték a hipotéziseket. Megfigyelheti, hogy a gravitáció az uralkodó erő az univerzumban a kozmológiai léptékben, és mivel az elektromágneses erő sokkal erősebb, mint a gravitációs erő, ha az univerzum nettó töltésű (pozitív vagy negatív), akkor képesek lesznek arra, hogy ilyen hatalmas távolságokon láthatja annak bizonyítékait. Ezen bizonyítékok hiánya alapján a kutatók azt hitték, hogy az univerzum töltöttségi szempontból semleges.

Vita tárgyát képezi még az is, hogy az univerzum mindig töltött semleges volt-e, vagy hogyan változott a világegyetem töltése a nagy robbantól kezdve. Ha az univerzum nettó töltéssel rendelkezne, akkor a tudósoknak képesnek kell lenniük arra, hogy minden elektromos terepi vonalon megfigyeljék tendenciáikat és hatásaikat oly módon, hogy ahelyett, hogy a pozitív töltésektől a negatív töltéshez kapcsolnának, soha nem érnek véget. E megfigyelés hiánya arra az érvre is rámutat, hogy az univerzumnak nincs nettó töltése.

Az elektromos fluxus kiszámítása töltéssel

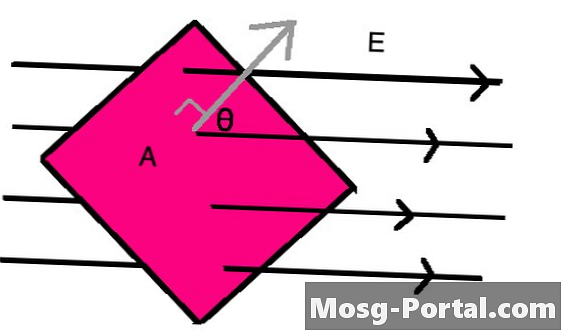
••• Syed Hussain Ather

A elektromos áram egy sík (azaz lapos) területen keresztül A egy elektromos mezőből E a mezõ szorozva a mezõre merõleges terület komponensével. Ennek a merőleges komponensnek a megszerzéséhez a mező és az érdekes sík közötti szög koszinuszát használja a fluxus képletében, amelyet Φ = EA kötözősaláta(θ), ahol θ a területre merőleges vonal és az elektromos mező iránya közötti szög.

Ez az egyenlet, úgynevezett Gausss törvény, azt is elmondja neked, hogy az ilyen felületeken, amelyeket hívsz Gauss felületek, bármilyen nettó töltés a sík felületén helyezkedik el, mert ehhez szükséges lenne az elektromos mező létrehozása.

Mivel ez a fluxus számításához használt felület geometriájától függ, az alakjától függ. Kör alakú terület esetén a fluxus terület A lenne π_r_² val vel r a kör sugaraként, vagy egy henger ívelt felületén a fluxus terület legyen Ch amiben C a hengerfelület kerülete és h a hengerek magassága.

Töltés és statikus áram

Statikus elektromosság akkor merül fel, ha két tárgy nincs elektromos egyensúlyban (vagy elektrosztatikus egyensúly), vagy, hogy az egyik tárgyról a másikra nettó töltés áramlik. Ahogy az anyagok egymással szemben dörzsölnek, a töltések átadódnak egymás között. A szőnyegen lévő zokni vagy a felfújt léggömb gumiabroncsa dörzsölése előidézheti ezeket az áramforrásokat. A sokk visszatéríti ezeket a többletköltségeket, hogy helyreálljon az egyensúlyi állapot.

Elektromos vezetők

Egy a karmester (anyag, amely áramot továbbít) elektrosztatikus egyensúlyban, a belső elektromos mező nulla, és a felületén levő nettó töltésnek elektrosztatikus egyensúlyban kell maradnia. Ennek oka az, hogy ha lenne egy mező, akkor a vezetőben lévő elektronok a mezőre reagálva újra eloszlanak vagy újra igazodnának. Ilyen módon törölnének bármilyen mezőt azonnali létrehozásával.

Az alumínium és a réz huzal az áramlás továbbításához használt általános vezető anyag, gyakran használnak ionvezetőket is, amelyek olyan megoldások, amelyek szabadon lebegő ionokat használnak, hogy a töltés könnyen átfolyhasson. Félvezetők, például a chipek, amelyek lehetővé teszik a számítógépek működését, szintén szabadon keringő elektronokat használnak, de nem olyan sok, mint a vezetők. Az olyan félvezetők, mint a szilícium és a germánium, több energiát igényelnek, hogy a töltések keringjenek, és általában alacsony vezetőképességgel rendelkeznek. Ellentétben, szigetelők például a fa, ne hagyja, hogy a töltés könnyen átfolyjon rajtuk.

Nincs mező belül, egy olyan gauss felületnél, amely csak a vezető felületén fekszik, a mezőnek mindenhol nullának kell lennie, hogy a fluxus nulla legyen. Ez azt jelenti, hogy a vezetőben nincs nettó elektromos töltés. Ebből levonható, hogy a szimmetrikus geometriai struktúrák, például a gömbök esetében a töltés egyenletesen oszlik el a Gauss felületén.

Gausss törvény más helyzetekben

Mivel a felület nettó töltésének elektrosztatikus egyensúlyban kell maradnia, minden elektromos mezőnek merőlegesnek kell lennie a vezető felületére, hogy az anyag töltéseket továbbítson. A Gausss-törvény lehetővé teszi, hogy kiszámítsa az elektromos mező nagyságát és a vezető fluxusát. A vezető belsejében lévő elektromos mezőnek nullának kell lennie, és kívülről merőlegesnek kell lennie a felületre.

Ez azt jelenti, hogy egy hengeres vezető számára, amelynek mezője merőleges szögben sugárzik a falaktól, a teljes fluxus egyszerűen 2_E__πr_² elektromos mezőhöz E és r a hengeres vezető kör alakú felületének sugara. A felület nettó töltését is felhasználhatja a σ, a töltési sűrűség egységnyi területenként, szorozva a területtel.