Tartalom
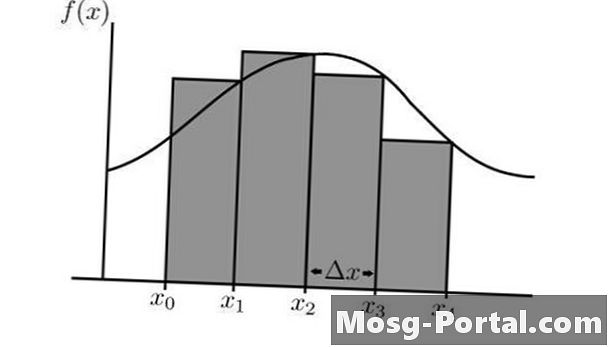
A Riemann-összeg a két X érték közötti matematikai görbe alatti terület közelítése. Ezt a területet téglalapok sorozatával közelítjük meg, amelyek szélessége a választott X delta és a kérdéses függvényből származtatott magasság, f (X). Minél kisebb a X delta, annál pontosabb lesz a közelítés. A magasság az f (X) értékéből vehető le a téglalap jobb, közepén vagy bal oldalán. Megtanulhatja, hogyan kell kiszámítani a bal oldali Riemann-összeget.
Keresse meg az f (X) értékét az első X értéknél. Példaként vegyük fel az f (X) = X ^ 2 függvényt, és a görbe alatti területet közelítjük 1 és 3 között 1 X delta-val; 1 ebben az esetben az első X érték, tehát f (1) = 1 ^ 2 = 1.
Szorozzuk meg a magasságot, az előző lépésben leírtak szerint, X delta-val. Ez megadja az első téglalap területét. Például 1 x 1 = 1.
Adja hozzá az X X értéket az első X értékhez. Ez megadja az X értéket a második téglalap bal oldalán. Például 1 + 1 = 2.
Ismételje meg a fenti lépéseket a második téglalapra. A példát folytatva, f (2) = 2 ^ 2 = 4; 4 x 1 = 4. Ez a példa második téglalapjának a területe. Folytassa ezen a módon, amíg el nem éri a végső X értéket. Például csak két téglalap van, mert 2 +1 = 3, ami a mérendő tartomány vége.
Adja hozzá az összes téglalap területét. Ez a Riemann-összeg. Befejezve a példát, 1 + 4 = 5.