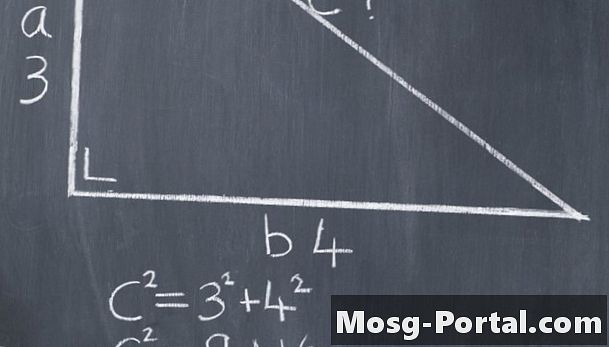
Tartalom
A hipoténus a derékszögű háromszög leghosszabb oldala. Ez a derékszögtől közvetlenül ellentétes oldal, és a hallgatók először a középiskolai években kezdik el megtanulni ezt a kifejezést a geometriaban. Megtalálhatja a hosszúságot, ha megadják a háromszög másik két oldalát, vagy egy szögmértéket és egy oldalhosszt.
Pitagorasz tétel
Egy derékszögű háromszögben a 90 fokos szöget létrehozó két oldalt lábaknak nevezzük, a hosszú oldalt, amely azokat összeköti, hipotenusznak nevezzük. Megtalálhatja a hipotenusz hosszát két lábból vagy egy lábból, és egy szögmértéket. A Pitagorasz-tétel egy képlet, amellyel meg lehet találni a jobb oldali háromszög egyik oldalának hosszát, ha két oldalt adnak meg. A képlet általában: a ^ 2 + b ^ 2 = c ^ 2, ahol a és b a lábak, és c a hipotenusz. Ha adnak a és b, akkor ezekkel és néhány algebrával megkeresheti a hipotenusz hosszát. Bármelyik változó is jelöli a hipoténust, az oldal c lesz a Pythagorai tétel képletében.
Csatlakoztasd
Egy derékszögű háromszög problémájának megoldásához mindig meg kell találnia egy háromszög hiányzó oldalát a másik két oldal használatával. A hipotenusz megtalálásához dugja be az a és b értékeket. Például nézzen meg egy háromszöget, amelynek oldala 3 és 4. Ha beilleszti őket a 3 ^ 2 + 4 ^ 2 = c ^ 2 képletbe, és egyszerűsíti, akkor 9 + 16 = c ^ 2 értéket kap. A 9 + 16 hozzáadásával 25 = c ^ 2 lesz.
Oldja meg az egyenletet
Miután négyzetbe tette a lábakat, és összeillesztette őket, önmagában még mindig c-nek kell lennie. Ha önmagában egy változót szeretne kapni az egyenletben, akkor alkalmazza az algebrai kardinális szabályt: bármit is csinálsz az egyenlet egyik oldalán, a másik oldalon is. Ebben az esetben önmagában "c" -re van szüksége, mivel ez a hipoténusz hossza. Ha a négyzetgyökét 25-nek vesszük, akkor kapjuk a c ^ 2 négyzetgyökét: c = 5.
Hármas háromszögek
A Pitagorói háromszögek olyan háromszögek, amelyek mindkét oldalán egész számmal rendelkeznek, és számítások nélkül felhasználhatók egyes háromszögek hipotenuszának meghatározására. Sokféle háromszög létezik, de a leggyakoribb a 3-4-5 és az 5-12-13 háromszög. Ezek az oldalhosszok lehetnek tényezők a nagyobb háromszögekben, ám ezek mindig egyenletes hármasra csökkennek. Például, ha 10 és 24 lábhosszúságú, csatlakoztathatja őket az egyenlethez, és a 10 ^ 2 + 24 ^ 2 négyzetgyökét megkaphatja. Ha azonban ismeri a hármasokat, akkor észreveszi, hogy a 10 és a 24 kétszer 5 és 12, tehát a hipotenusznak kétszer 13 vagy 26 kell lennie.