Egy egyenlő oldalú háromszög egy háromszög, amelynek mindhárom oldala azonos hosszúságú. Egy kétdimenziós sokszög, például egy háromszög felszíni területe a sokszög oldalainak teljes területe. Egy egyenlő oldalú háromszög három szöge ugyanolyan nagyságrendű az euklideszi geometriában. Mivel az euklideszi háromszög szögeinek teljes mértéke 180 fok, ez azt jelenti, hogy egy egyenlő oldalú háromszög szögeinek mind 60 fokát kell mérniük. Egy egyenlő oldalú háromszög területét akkor lehet kiszámítani, amikor az egyik oldalának hossza ismert.

Határozzuk meg a háromszög területét, amikor az alap és a magasság ismertek. Vegyünk bármilyen két azonos háromszöget, amelynek alapja s és h magassága. E két háromszöggel mindig alakíthatunk párhuzamos képet az alap és a h magasságról. Mivel a párhuzamos ábra területe s x h, a háromszög A területe ezért ½ s x h.

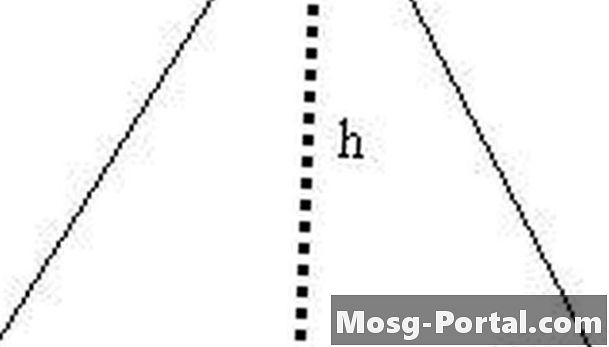
Az egyenlő oldalú háromszöget alakítson két jobb háromszögbe a h vonallal. A jobb oldali háromszög egyikének hipotenuza s egyik hosszú, egyik lába h hosszú, a másik lába s / 2 hosszú.
Fejezzük ki h-t s-ben. A 2. lépésben kialakított derékszögű háromszög használatával tudjuk, hogy s ^ 2 = (s / 2) ^ 2 + h ^ 2 a Pitagóra képlettel. Ezért h ^ 2 = s ^ 2 - (s / 2) ^ 2 = s ^ 2 - s ^ 2/4 = 3s ^ 2/4, és most már h = (3 ^ 1/2) s / 2.
Cserélje ki a 3. lépésben kapott h értéket az 1. lépésben kapott háromszög terület képletére. Mivel A = ½ sxh és h = (3 ^ 1/2) s / 2, most A = ½ s (3 ^ 1/2) s / 2 = (3 ^ 1/2) (s ^ 2) / 4.
A 4. lépésben kapott egyenlő oldalú háromszög területének képletével keresse meg a 2. hosszú oldalú egyenlő oldalú háromszög területét. A = (3 ^ 1/2) (s ^ 2) / 4 = (3 ^ 1/2 ) (2 ^ 2) / 4 = (3 ^ 1/2).