Tartalom
- A parabola
- Menaechmus matematikus
- A "Parabola" név
- Galileo és lövedékes mozgás
- Parabolikus reflektorok
- Függesztő hidak
Matematikai görbéket, például a parabolát nem találták ki. Inkább felfedezték, elemezték és felhasználták őket. A parabolának számos matematikai leírása van, hosszú és érdekes története van a matematikában és a fizikában, és manapság számos gyakorlati alkalmazásban használják.
A parabola
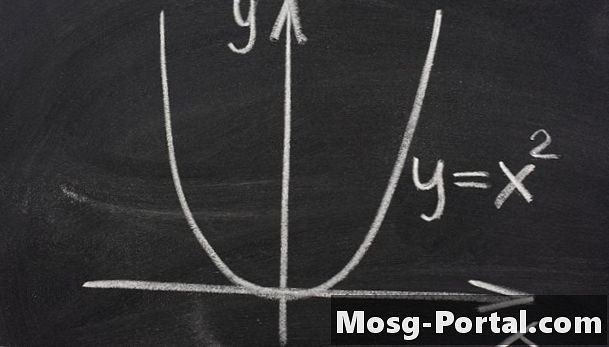
A parabola egy folytonos görbe, amely úgy néz ki, mint egy nyitott tál, ahol az oldalak végtelenül felmegynek. A parabola egyik matematikai meghatározása azon pontok halmaza, amelyek ugyanolyan távolságra vannak a rögzített ponttól, amelyet fókusznak hívnak, és egy vonalt, az úgynevezett irányt. Egy másik meghatározás az, hogy a parabola egy speciális kúpos szakasz. Ez azt jelenti, hogy egy görbe látható, ha egy kúpot szelsz át. Ha a kúp egyik oldalával párhuzamosan szeletelsz, akkor egy parabolát látsz. A parabola szintén az y = ax ^ 2 + bx + c egyenlettel definiált görbe, ha a görbe az y tengely körül szimmetrikus. Általánosabb egyenlet létezik más helyzetekre is.
Menaechmus matematikus
A görög matematikus, Menaechmus (a negyedik század közepén, Kr. E.) Az a hitele, hogy felfedezték, hogy a parabola kúpos szakasz. Arra is számít, hogy parabolákat használ a geometriai konstrukció megtalálásának problémájára a kettõs gyökérgyökér számára. Menaechmus nem tudta megoldani ezt a problémát egy konstrukcióval, de megmutatta, hogy megoldást találhat két parabolikus görbe metszésével.
A "Parabola" név
Perga (Apollonius, a harmadik-második évszázadok óta) görög matematikusát a parabola elnevezésével kapják meg. A "parabola" a "pontos alkalmazás" görög szóból származik, amely az online etimológia szótár szerint "azért keletkezik, mert egy adott területet egy adott területre" alkalmaznak "egy egyenesre."
Galileo és lövedékes mozgás
A Galileo idején ismert volt, hogy a testek egyenesen a négyzetszabály szerint esnek le: A megtett távolság arányos az idő négyzetével. A lövedék mozgásának általános útjának matematikai jellege azonban nem volt ismert. Az ágyúk megjelenésével ez fontos kérdéssé vált. Felismerve, hogy a vízszintes és a függőleges mozgás egymástól függetlenek, a Galileo megmutatta, hogy a lövedékek parabolikus úton haladnak. Elméletét végül Newton gravitációs törvényének különleges eseteként érvényesítették.
Parabolikus reflektorok
A parabolikus reflektor képes fókuszálni vagy koncentrálni az egyenesen rá érkező energiát. A műholdas TV, a radar, a mobiltelefon-tornyok és a hanggyűjtők mind a parabolikus reflektorok fókuszálási tulajdonságait használják.A hatalmas rádióteleszkópok koncentrálják a gyenge jeleket az űrből, hogy képeket készítsenek távoli tárgyakról, és sok hatalmas is használatban van. A visszaverő fénytávcsövek ezen az elven is működnek. Sajnos az a mese, hogy Archimédész egy görög hadseregnek parabolikus tükrök használatával segített lángot gyújtani a megszálló római hajók számára, akik 213-ban B.C.-t támadtak Syracuse városába. valószínűleg nem több, mint legenda. A fókuszálási folyamat fordított irányban is működik: a tükör felé a fókuszból kibocsátott energia egy nagyon egyenes egyenes sugárnyal tükröződik. A lámpák és az adóegységek, például a radar és a mikrohullámok, a fókuszban lévő forrásból visszatükrözött irányított energia sugarai bocsátanak ki.
Függesztő hidak
Ha megtartja a kötél két végét, akkor leesik egy görbe felé, amelyet vezetõvezetéknek hívnak. Vannak, akik tévedik ezt a görbét egy parabolához, de valójában nem. Érdekes, hogy ha a súlyokat akasztja a kötélről, akkor a görbe alakját úgy változtatja meg, hogy a felfüggesztés pontjai parabolara, nem pedig a felsővezetékre vonatkozzanak. Tehát a felfüggesztő hidak függő kábelei valójában parabolákat képeznek, nem pedig felsővezetékeket.