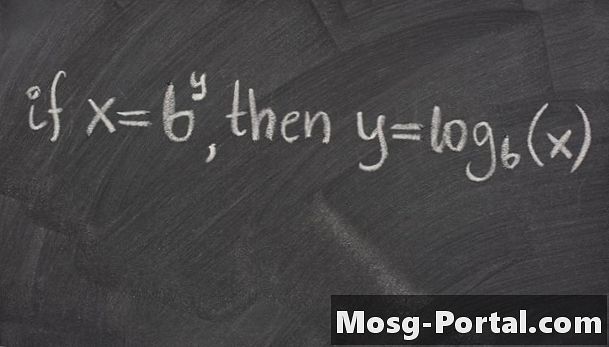
Tartalom
A logaritmus egy matematikai függvény, amely szorosan kapcsolódik az exponenciákhoz. Valójában a logaritmus az exponenciális függvény inverze. Az általános forma a log_b (x), amely a következőt jeleníti meg: „x napló bázisa”. Gyakran a bázis nélküli napló a 10. alap naplóba sorolja a log_10 értéket, az ln pedig a „természetes napló” log_e, ahol e fontos transzcendentális szám. , e = 2.718282 .... Általában a log_b (x) kiszámításához egy számológépet használ, de a logaritmusok tulajdonságainak ismerete segíthet bizonyos problémák megoldásában.
Tulajdonságok
A logaritmikus bázis meghatározása log_b (b) = 1. A logaritmikus függvény meghatározása: y = b ^ x, akkor log_b (y) = x. További fontos tulajdonságok: log_b (xy) = log_b (x) + log_b (y), log_b (x / y) = log_b (x) - log_b (y) és log_b (x ^ y) = ylog_b (x). Ezekkel a tulajdonságokkal segíthet kiszámítani a logaritmusokat különböző helyzetekben.
Gyors trükkök
Időnként gyorsan kiszámolhatja a log_b (x) értéket, ha meg tudja válaszolni a b ^ y = x problémát. Log_10 (1000) = 3, mert 10 ^ 3 = 1000. Log_4 (16) = 2, mert 4 ^ 2 = 16. Log_25 (5) = 0,5, mert 25 ^ (1/2) = 5. Log_16 (1/2) = -1/4, mert 16 ^ (- 1/4) = 1/2, vagy (1/2) ^ 4 = 1/16. A log_b (xy) képlettel log_2 (72) = log_2 (8 * 9) = log_2 (8) + log_2 (9) = 3 + log_2 (9). Ha becsüljük a log_2 (9) ~ log_2 (8) = 3 értéket, akkor log_2 (72) ~ 6. A tényleges érték 6,2.
Alapok megváltoztatása
Tegyük fel, hogy ismeri a log_b (x) -ot, de szeretné tudni a log_a (x) -ot. Ezt hívják az alapok megváltoztatásának. Mivel a ^ (log_a (x)) = x, akkor írni log_b (x) = log_b. A log_b (x ^ y) = ylog_b (x) használatával ezt át lehet alakítani log_b (x) = log_a (x) log_b (a) értékre. Ha mindkét oldalt el osztja log_b (a) -vel, akkor a log_a (x) esetén megoldható: log_a (x) = log_b (x) / log_b (a). Ha van egy számológép, amely 10 naplót készít, de szeretné tudni, hogy a log_16 (7.3), akkor megtalálja ezt a log_16 (7.3) = log_10 (7.3) / log_10 (16) = 0.717 alapján.