
Az autokorreláció statisztikai módszer, amelyet idősorok elemzéséhez használnak. A cél két érték korrelációjának mérése ugyanazon adatkészletben, különböző időpontokban. Noha az időadatokat nem használják az automatikus korreláció kiszámításához, az időnkénti növekedésnek azonosnak kell lennie a lényeges eredmények elérése érdekében. Az autokorrelációs együttható két célt szolgál. Felismeri a nem véletlenszerűségeket egy adatkészletben. Ha az adatkészletben szereplő értékek nem véletlenszerűek, akkor az automatikus korreláció segíthet az elemzőnek a megfelelő idősor-modell kiválasztásában.
Számítsa ki az elemzett adatok átlagát vagy átlagát. Az átlag az összes adatérték összege, elosztva az adatértékek számával (n).
Döntse el a számítási késleltetést (k). A lemaradási érték olyan egész szám, amely jelzi, hogy hány időlépést választ el az egyik érték a másiktól. Például az (y1, t1) és (y6, t6) közötti késés öt, mert a két érték között 6 - 1 = 5 idő lépés van. A véletlenszerűség tesztelésekor általában csak egy autokorrelációs együtthatót számít ki, ha késleltetés k = 1, bár más késési értékek is működnek. A megfelelő idősor-modell meghatározásakor kiszámítania kell az autokorrelációs értékek sorozatát, mindegyikhez külön-külön különbözõ késési értéket használva.
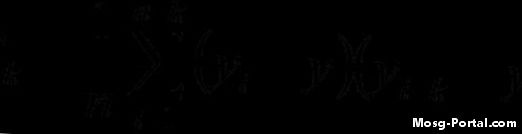
Számítsa ki az autovariáns függvényt az adott képlet alapján. Például, ha a harmadik iterációt (i = 3) egy k = 7 késleltetés alapján számította ki, akkor az iteráció számítása így néz ki: (y3 - y-bar) (y10 - y-bar) Az összes "i" értékét, majd vegye össze az összeget és ossza meg az adatkészletben szereplő értékek számával.
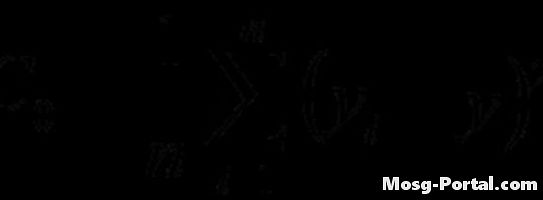
Számítsa ki a varianciafüggvényt az adott képlet segítségével. A számítás hasonló az autovariáns függvény számításához, de a késést nem használják.

Osszuk meg az autokvariancia függvényt a variancia függvénnyel, hogy megkapjuk az autokorrelációs együtthatót. Megkerülheti ezt a lépést a két funkció képletének elosztásával, amint az ábrán látható, de sokszor szüksége lesz autocovariációra és varianciára más célokra, így célszerű ezeket külön-külön kiszámítani.